3D confocal Raman microscopy is a powerful research technique that can provide precise chemical information with micron-range spatial resolution from subsurface inclusions and layers within a sample
However, when using a metallurgical objective lens, the refractive index mismatch between air and the sample leads to spherical aberration, which causes depth axis compression and degradation in the axial resolution and spectral sensitivity with increasing depth. This can lead to significant errors in determining the depth and thickness of regions of interest in a sample.
In this Technical Note, we show that immersion objectives (e.g. water and oil) reduce refractive index mismatching and, therefore, spherical aberration. By analysing a multi-layer polymer sample, we demonstrate that immersion objectives improve the spatial accuracy and spectral sensitivity of 3D confocal Raman microscopy.
To understand spherical aberration, let’s consider a 3D confocal Raman microscopy experiment where we attempt to focus the laser to a depth, d, into a sample using a metallurgical objective, Figure 1. To do this, we would focus on the sample surface at the objective focal length, f, and then raise the sample by d using the microscope stage. However, the laser would not be focused at d. This is because the refractive index of the sample, n2 is larger than the refractive index of air, n1, and the refraction of light rays in the sample will differ based on what part of the objective they passed through.
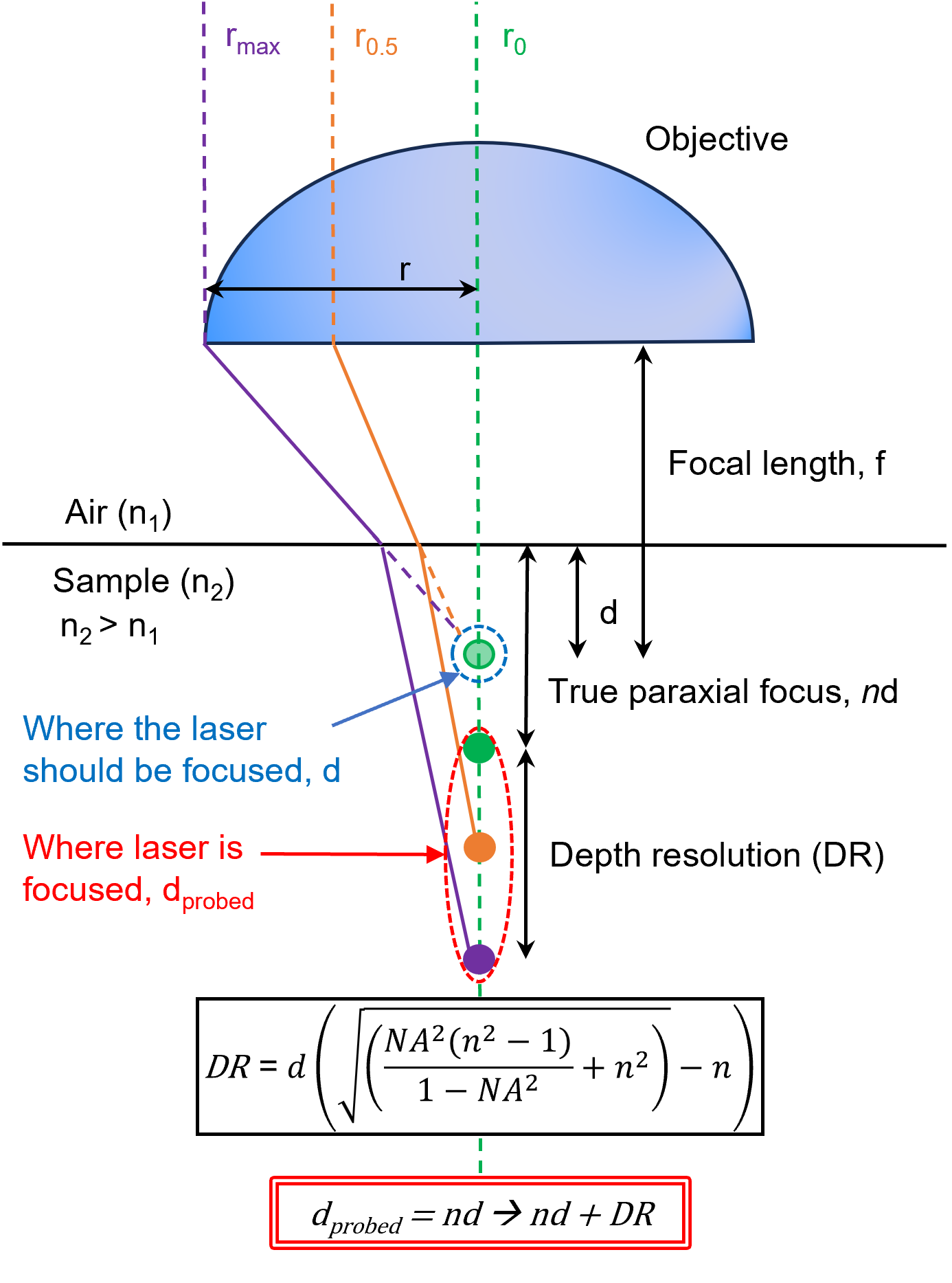
Figure 1. Depiction of spherical aberration when attempting to focus a laser into a sample with a metallurgical objective lens of focal length f. If one attempts to focus the laser at a distance d, the focal point is moved deeper into the sample and the laser intensity becomes spread out axially by refraction.
The paraxial ray, which is represented in green, that passes through the very centre of the objective, will be focused at a depth nd, where n represents the index mismatch between air and the sample.1 The orange ray, which originates halfway between the centre and the edge of the lens and impacts the sample interface at an angle, is focused deeper than the paraxial ray because of refraction. This is described by Snell’s Law, Equation 1.
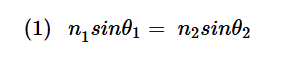
To maintain equivalence, if the angle of incidence, θ1, increases, the angle of refraction, θ2, must also increase. The purple ray, which originates from the very edge of the objective, will be focused even deeper than the orange ray because it enters the sample further away from the paraxial ray and is also refracted.
The cumulative effect of these multiple refraction events on the laser focus here is that it will be deeper than d, and the laser intensity will become spread out axially by a distance DR, which is described in Figure 1. We can, therefore, conclude that the laser intensity would be confined within the range between nd and nd + DR, instead of focusing to a point at d.2 Also, since DR is proportional to d, if one attempts to focus further into the sample by increasing d, the laser’s point spread function (PSF) broadens even more in the axial direction.
We have established that spherical aberration causes the laser to focus deeper into a sample than intended, and the focus elongates along the optical axis. These effects are both amplified as the target depth increases.
In this section, we will show that this causes erroneous depth scale compression in 3D Raman images, and we will demonstrate that depth compression can be mitigated by using an immersion objective where the refractive index of the immersion medium matches that of the sample. Minimisation of the refractive index discontinuity at the sample surface means that light rays passing through all points on the objective will focus more closely to d, Figure 2.
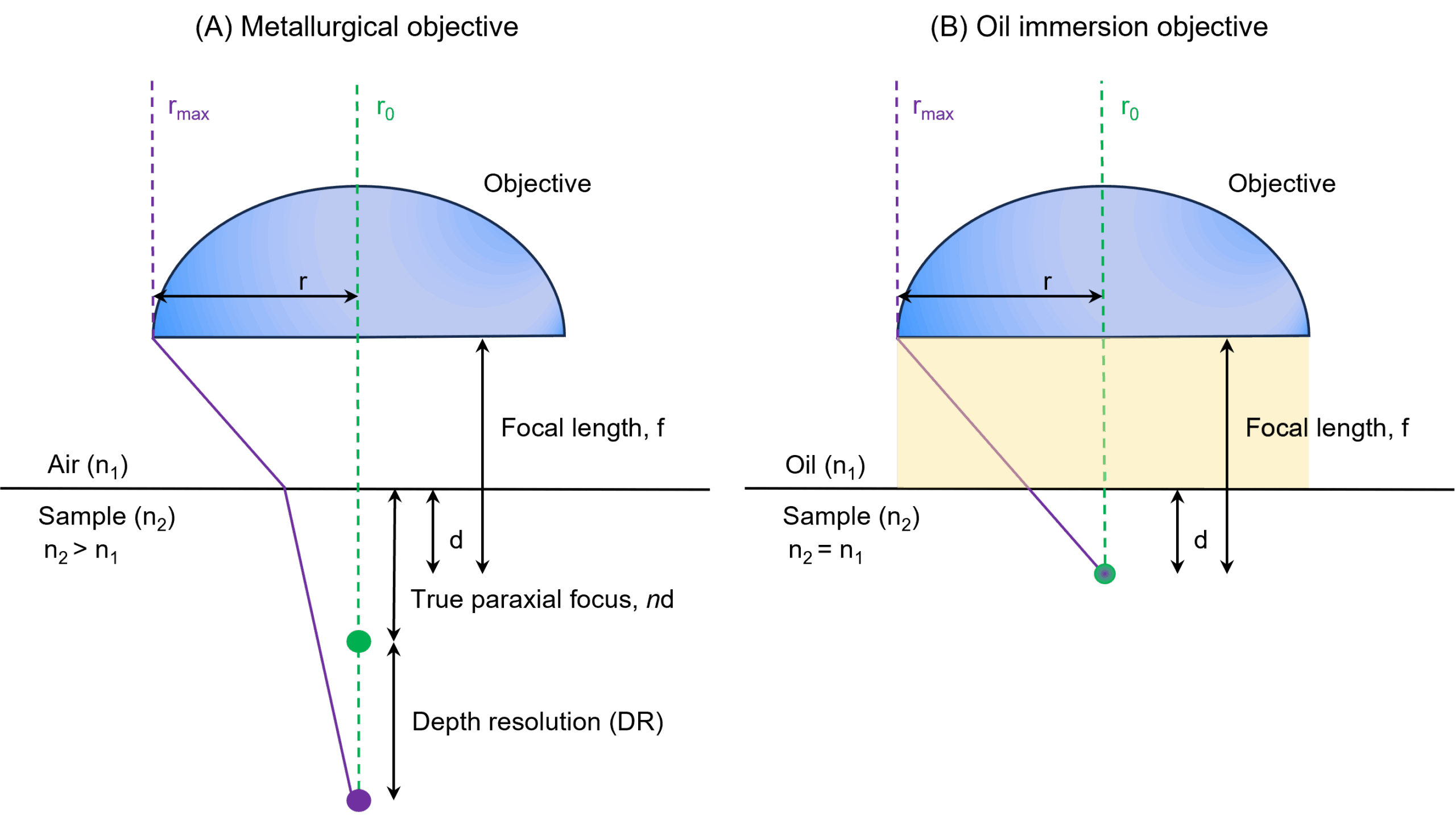
Figure 2. The focal depth and axial resolution obtained when using a (A) metallurgical and (B) oil immersion objective for 3D confocal Raman microscopy.
To highlight the effects of spherical aberration on Raman images and its removal using immersion medium index matching, a transdermal nicotine patch containing multiple polymeric layers was analysed using 3D Raman imaging on an RMS1000 Confocal Multimodal Microscope, first with a 100X 0.9 NA metallurgical objective, and then with a 100X 1.20 NA oil immersion objective. The spectral and imaging parameters for both mapping experiments were equivalent. In both instances, a confocal pinhole diameter of 100 μm was used. A small confocal pinhole diameter reduces the collection volume within the sample and improves the axial spatial resolution during 3D mapping.
XZ slices from 3D Raman images of the same volume collected using metallurgical and oil immersion objectives are shown in Figure 3. In both cases, six discrete layers were identified using spectral matching based on the Pearson correlation algorithm in Ramacle®.
In the metallurgical objective image, Figure 3A, the entire thickness of the film is shown to be 150 μm. In the oil immersion objective image, Figure 2B, the entire thickness of the film is shown to be 240 μm. Each layer underneath the red surface layer is also shown to be at a shallower depth and compressed in Figure 3A relative to Figure 3B.
In Figure 3A, the pink layer spectral matching appears heterogeneous, as observed in the varying shades of pink throughout the layer. This was attributed to the decrease in the signal-to-noise ratio of the spectra with increasing depth, which will be discussed later.
This discrepancy is due to spherical aberration when using the metallurgical objective, which makes the focus deeper than intended and, therefore, compresses the depth scale in the resulting image. Clearly, the use of an oil immersion objective effectively mitigates spherical aberration-induced depth compression in 3D Raman imaging.

Figure 3. XZ slices from 3D Raman images recorded from the same volume in a transdermal patch using a (A) metallurgical and (B) oil immersion objective lens.
An immersion objective also provides superior spectral sensitivity to a metallurgical objective in Raman microscopy. This applies to the measurement of materials on the surface of a sample, and at depth.
The sensitivity of surface measurements is improved when using an immersion objective because it generally has a higher NA than a metallurgical objective. The numerical aperture of an objective is a dimensionless number that characterises the range of angles over which the objective can emit and collect light. It is defined in Equation 2; here, n is the refractive index of the medium in which the lens is immersed, and θ is the half-angle of the maximum cone of light that can enter or exit the lens. 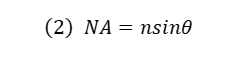
Therefore, a higher NA will correspond to a larger maximum cone half-angle for a set of objectives designed for immersion in the same medium (e.g., air, water, oil). Using a high NA objective increases the collection efficiency of Raman scatter because it allows for the collection of photons scattered at an oblique angle, which would be lost when using low NA objectives. The result of higher collection efficiency is higher spectral sensitivity. Figure 4 shows spectra recorded from the surface (red) layer of the transdermal patch with the two objectives, but otherwise identical conditions. The spectrum recorded with the objective is significantly more intense, with a 2.9-fold greater signal-to-noise ratio.
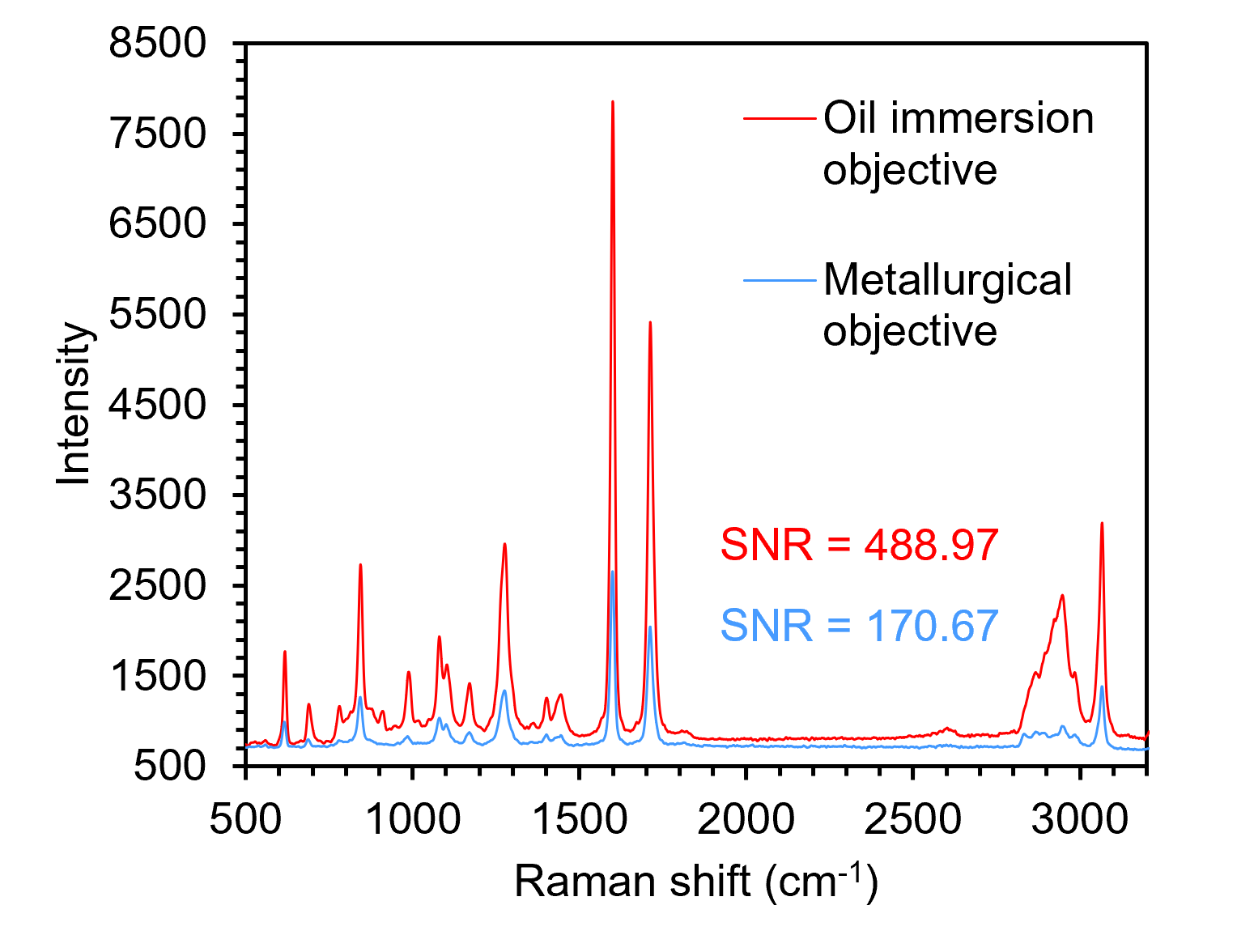
Figure 4. Spectra recorded from the surface of the transdermal patch with oil immersion (red) and metallurgical (blue) objectives.
In a confocal Raman microscope, only photons that are generated in and pass through the confocal pinhole collection volume can be detected. We already established that when performing 3D confocal Raman microscopy with a metallurgical objective and attempting to focus at d, axial elongation of the laser intensity will occur, and the PSF would be spread out within a range between nd and nd + DR. This reduces the power density of the laser at any point within the sample, including the confocal pinhole collection volume, Figure 5. Since Raman intensity is proportional to the power of the excitation source, the spectral sensitivity achieved would decrease.4
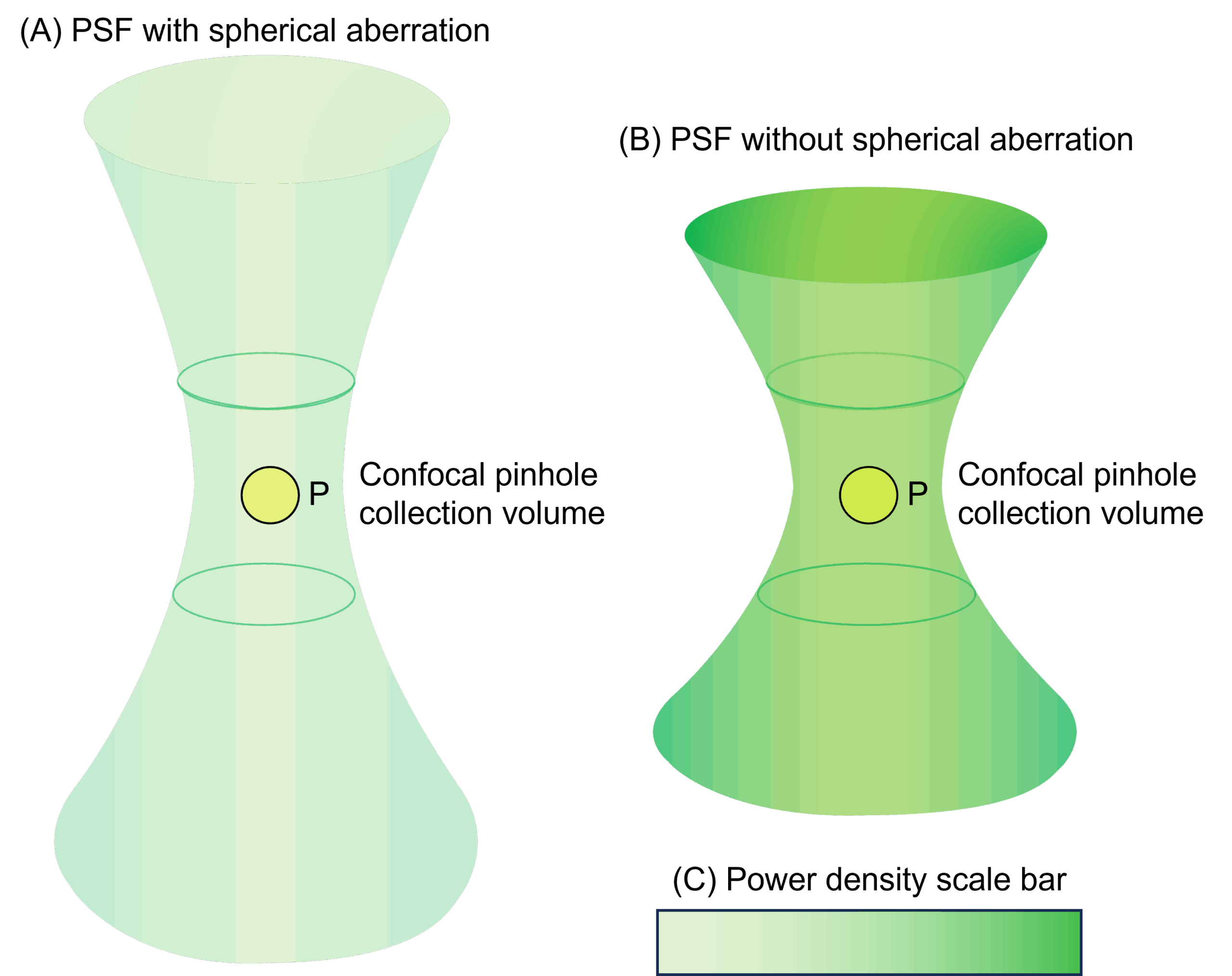
Figure 5. The volume and power density of the PSF within a sample (A) with and (B) without spherical aberration. (C) A scale bar showing the difference in power density between (A) and (B).
When probing at depth with an oil immersion objective, the PSF does not elongate due to spherical aberration because n1 is approximately equal to n2. This means that the power density of the laser within the confocal pinhole collection volume is high, and greater spectral sensitivity can be obtained. Figure 6 shows spectra recorded from the lowest (pink) layer of the transdermal patch with the two objectives, but otherwise identical conditions. Again, the spectrum recorded with the oil immersion objective is . There is a 3.7-fold improvement in signal-to-noise ratio when using an oil immersion lens.
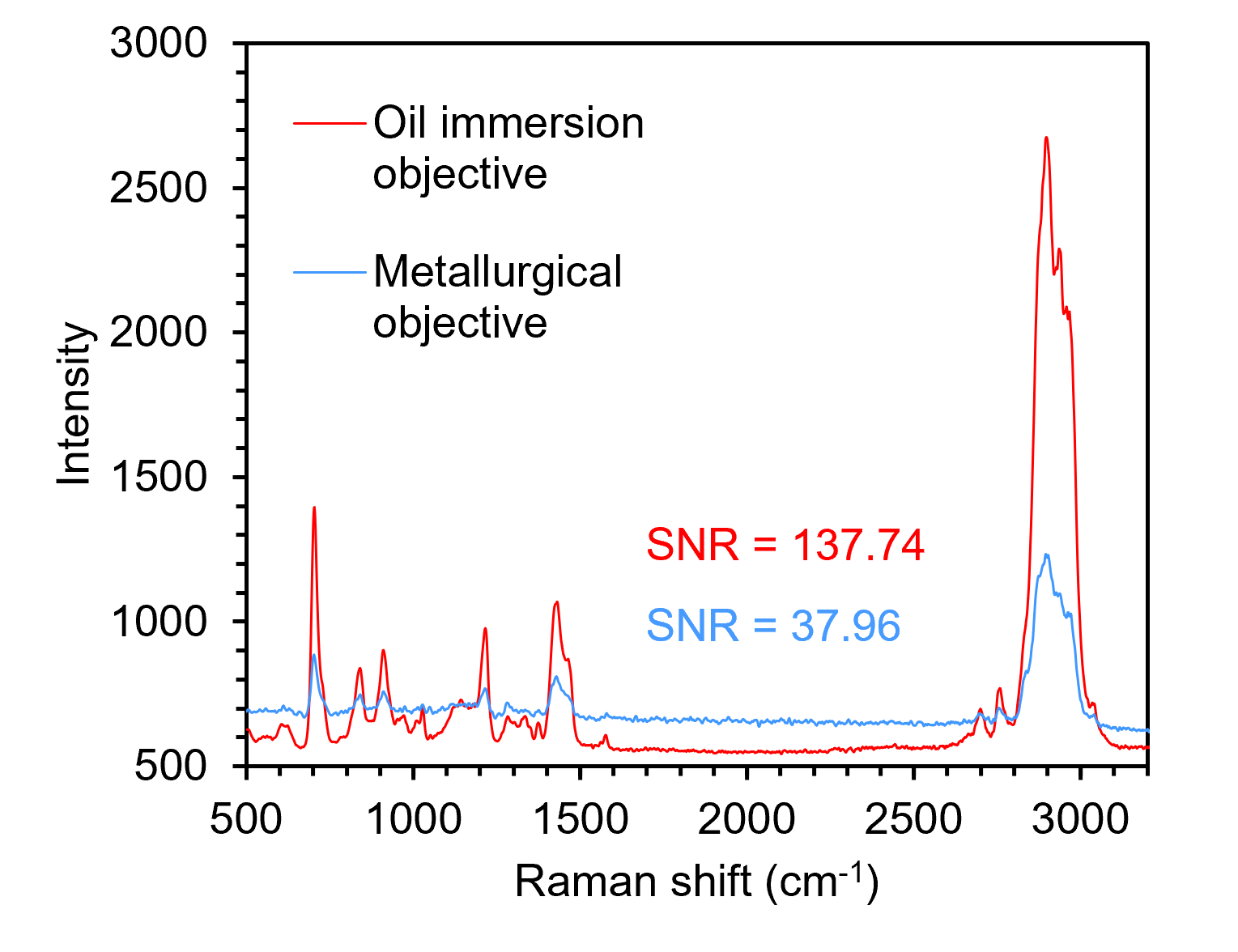
Figure 6. Spectra recorded from the pink subsurface layer of the transdermal patch with oil immersion (red) and metallurgical (blue) objectives.
Immersion objectives significantly enhance 3D confocal Raman microscopy by minimizing spherical aberration, which improves both spatial accuracy and spectral sensitivity. This leads to more accurate depth profiling and stronger Raman signals, particularly in subsurface layers.



