The spot size that a laser can be focused down to in Raman or fluorescence microscopy is an important parameter that depends on the wavelength of the laser and the properties of the microscope’s objective lens.
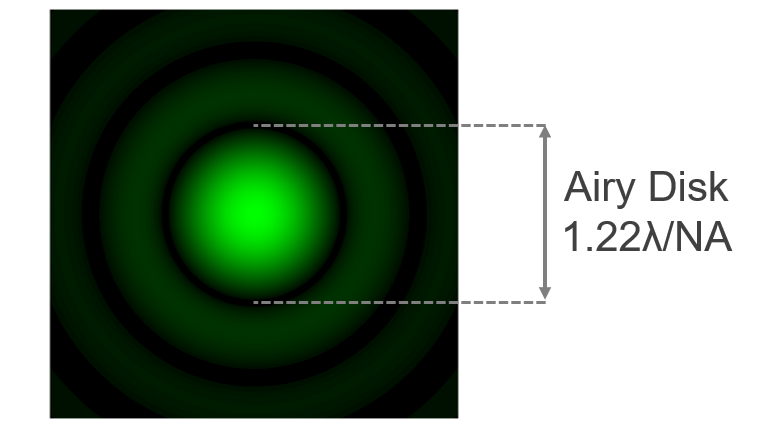
The first question that could be asked is what is meant by ‘spot size’? When light passes through any aperture (in this case the microscope objective lens) diffraction occurs. The diffraction pattern that results from uniformly illuminating a circular aperture is called the Airy pattern and is shown in Figure 1. It consists of a bright central circle known as the Airy disc which contains 84% of the total light intensity, with the remaining 16% distributed across a series of progressively less intense concentric rings.
Figure 1: Simulated Airy pattern of a laser spot and the different definitions of spot size.
The diameter of the Airy disc (defined as the distance between the first minima in the diffraction pattern) is what is generally meant by ‘spot size’ in microscopy. The diameter depends on the wavelength of the laser light and the numerical aperture (NA) of the objective lens:
The lateral spatial resolution limit of a microscope is closely related to Eq. 1 and is obtained by replacing the 1.22 pre-factor with 0.61. This corresponds to the distance between the central maxima and first minima in the diffraction pattern and is known as the Rayleigh criterion.
The Airy disc diameter is not the only definition of spot size. Two other popular definitions are the width that the diffraction pattern falls to either half intensity (FWHM) or to 1/e2 intensity which are approximately given by:
The Airy disc represents the minimum spot size that is achievable and assumes a perfect optical system that is free of aberrations – which is never quite true in practice. More importantly, it also assumes that the rear aperture of the objective has been uniformly illuminated. Lasers typically have a narrower beam diameter than the objective rear aperture and do not have a uniform transverse intensity (typically possessing a Gaussian profile) and directly illuminating the objective with a laser will result in a larger spot size than predicted by Eq. 1.
The solution is to beam expand the laser so that its beam diameter is larger than the rear aperture of the objective in order to approximate uniform illumination – which is known as overfilling. The greater the degree of overfilling the better the approximation to uniform illumination and the closer the spot size is to Eq. 1. Overfilling comes at the cost of lowering the intensity of laser light reaching the sample and there is a trade-off between spatial resolution and power transmission through the objective.
The spot size depends on the laser wavelength (Eq. 1) with shorter wavelength lasers offering smaller spot sizes and improved spatial resolution. The spot sizes that can be achieved at three common Raman microscopy wavelengths using a high magnification air objective lens (100x 0.9 NA) are illustrated in Figure 2.
Figure 2: Simulation of the dependence of the spot size on laser wavelength through a 100x 0.9 NA objective lens.
The spot size also depends on the numerical aperture (NA) of the objective lens which is a measure of how oblique an angle of light can enter or exit the lens,
where n is the refractive index of the medium between the objective and the sample and α is the half angle the light cone entering/exiting the objective.
The NA depends on the construction of the objective and generally increases with increasing objective magnification. Standard air (n = 1) objectives are limited to an NA of <1, with higher NAs up to ~1.4 achievable with the use of immersion oil objectives due to the higher refractive index. The higher the NA the larger the acceptance angle of the objective and the smaller the spot size that can be achieved, which is illustrated in Figure 3 with three commonly used air objectives.
Figure 3: Simulation of the dependence of a 532 nm laser spot size on the numerical aperture of the objective lens.
One thing to note is Figure 3 contains somewhat of a simplification as the simulations assume that the rear aperture of all three objectives are uniformly illuminated. As discussed above, this is achieved by beam expanding and overfilling the rear aperture of the objective. However, the diameter of the rear aperture varies with objective magnification – with the rear aperture diameter decreasing as magnification increases. In multi-objective systems, the beam expansion is typically optimised for the high magnification objectives – where it matters more. Lower magnification objectives (such as the 20x 0.4 NA in Figure 3) with larger rear apertures are typically underfilled and the spot size and diffraction pattern will have more Gaussian character from the laser than shown here.
If you have enjoyed reading this article, why not sign up to our monthly newsletter via the button below or follow us on LinkedIn, Twitter or Facebook to keep up to date with our latest news and research.
