The Beer-Lambert Law (also called Beer’s Law) is a relationship between the attenuation of light through a substance and the properties of that substance. In this article, the definitions of transmittance and absorbance of light by a substance are first introduced followed by an explanation of the Beer-Lambert Law.
Consider monochromatic light transmitted through a solution; with an incident intensity of I0 and a transmitted intensity of I (Figure 1).
Figure 1: Transmission of light through a sample solution in a cuvette.
The transmittance, T, of the solution is defined as the ratio of the transmitted intensity, I, over the incident intensity, I0 and takes values between 0 and 1:
However, it is more commonly expressed as a percentage transmittance:
The absorbance, A, of the solution is related to the transmittance and incident and transmitted intensities through the following relations:
The absorbance has a logarithmic relationship to the transmittance; with an absorbance of 0 corresponding to a transmittance of 100% and an absorbance of 1 corresponding to 10% transmittance. Additional values of transmittance and absorbance pairings are given in Table 1. A visual demonstration of the effect that the absorbance of a solution has on the attenuation light passing through it is shown Figure 2, where a 510 nm laser is passed through three solutions of Rhodamine 6G with different absorbance.
Table 1: Absorbance and Transmittance Values:
| Model (VPL-) | 375 | 405 | 420 | 445 | 450 | 475 | 485 | 510 | 635 | 640 | 655 | 670 | 700 | 730 | 785 | 800 | 980 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Nominal Wavelength (±10 nm) | 375 | 405 | 420 | 445 | 450 | 475 | 485 | 510 | 635 | 640 | 655 | 670 | 700 | 730 | 785 | 800 | 980 |
| Typical CW Average Power (mW) | 30 | 25 | 55 | 15 | 30 | 25 | 30 | 15 | 35 | 35 | 15 | 10 | 15 | 15 | 35 | 40 | 10 |
| Minimum CW Average Power (mW) | 20 | 10 | 30 | 10 | 20 | 10 | 25 | 10 | 25 | 15 | 10 | 8 | 15 | 15 | 25 | 10 | 10 |
| Typical Peak Power (mW) * | 100 | 45 | 150 | 45 | 100 | 30 | 90 | 25 | 110 | 45 | 34 | 24 | 40 | 40 | 100 | 100 | 30 |
| Minimum Peak Power (mW) * | 60 | 30 | 100 | 30 | 85 | 20 | 60 | 20 | 80 | 30 | 30 | 16 | 30 | 30 | 70 | 20 | 20 |
Figure 2: Attenuation of a 510 nm laser through three solutions of Rhodamine 6G with different absorbance values at 510 nm. The yellow glow is the fluorescence emission at ~560 nm.
Absorbance is a dimensionless quantity and should, therefore, be unitless. However, it is quite common to see units of AU stated after the absorbance which are to said to either stand for arbitrary units or absorbance units. These units are redundant and should be avoided. Another common encounter is the use of the term optical density or OD in place of absorbance. Optical density is an older term that, in the context of absorption spectroscopy, is synonymous with absorbance; however, the use of optical density in place of absorbance is discouraged by the IUPAC.1
The Beer-Lambert law is a linear relationship between the absorbance and the concentration, molar absorption coefficient and optical path length of a solution:
The molar absorption coefficient is a sample dependent property and is a measure of how strong an absorber the sample is at a particular wavelength of light. The concentration is simply the moles L-1 (M) of the sample dissolved in the solution, and the optical path length is the width of the cuvette used for the absorbance measurement and is typically 1 cm.
The Beer-Lambert law states that there is a linear relationship between the concentration and the absorbance of the solution, which enables the concentration of a solution to be calculated by measuring its absorbance. To demonstrate this linear dependence five solutions of Rhodamine B in water were measured using the DS5 Dual Beam Spectrophotometer (Figure 3a) and from these absorption spectra, a linear calibration curve of the absorbance versus concentration was created (Figure 3b). Using this calibration curve the concentration of an unknown Rhodamine B solution can be determined by measuring its absorbance which is the main utility of the Beer-Lambert Law.
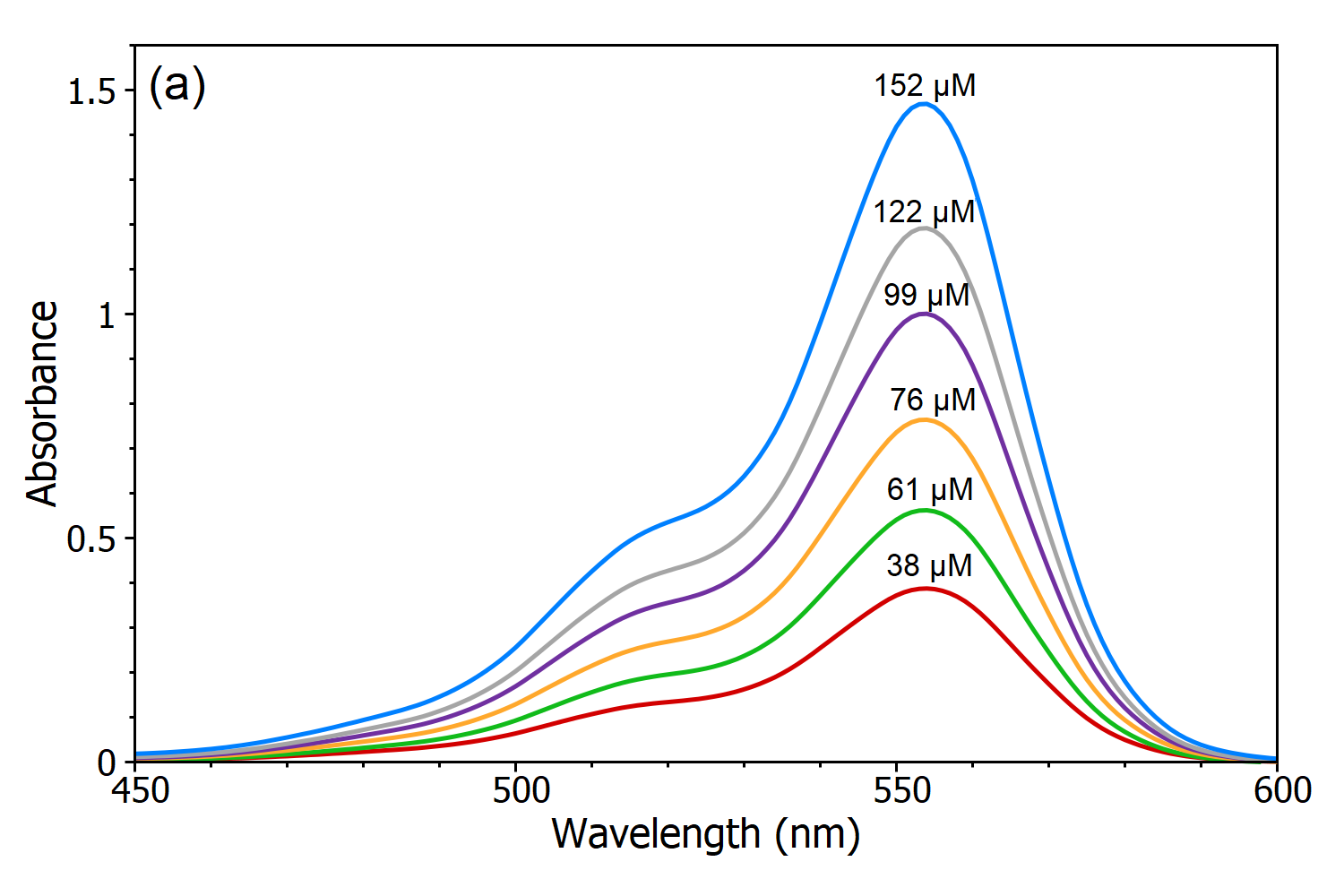
Figure 3 (a): Absorption spectra of Rhodamine B solutions with different concentrations in water measured using the DS5 Dual Beam Spectrophotometer. (b) Calibration curve of Rhodamine B in the water at measured at λmax.
For more information on the theory of optical spectroscopy, check out the frequently asked questions section on our blog.
Edinburgh Instruments range of high end fluorescence spectroscopy equipment are perfect for absorption/transmission measurements. Why not browse our range below:
If you have enjoyed reading our article on the Beer Lambert Law and would like to keep up to date with our latest articles, research and product news, why not sign up to our monthly eNewsletter via the Sign-Up button below. Alternatively, join us on your favourite social media channel via the buttons at the bottom of the page.
